Entries tagged as cryptography
aiglx 3d 4k assembler cacert ccc ccwn come2linux compiz darmstadt entropia essen games gentoo gentoo. compiz gpn gpn5 hacker hash linux md5 metacity mrmcd mrmcd100b mrmcd101b passwörter programming security server sha1 unicode utf-8 vortrag wiesbaden wine xgl xorg algorithm certificate eff observatory pss rsa ssl android ac100 cloudflare facebook https laptop notebook sha256 smartbook subnotebook tls toshiba ubuntu updates windowsxp apache certificates datenschutz datensparsamkeit encryption grsecurity itsecurity javascript karlsruhe letsencrypt mod_rewrite nginx ocsp ocspstapling openssl php revocation serendipity sni symlink userdir web web20 webhosting webmontag websecurity apt deb debian fedora gnupg gpg openpgp packagemanagement pgp rpm signatures badkeys fortigate fortinet leak privatekey braunschweig bsideshn cdu easterhegg gerthoffmann hannover internetausdrucker netzpolitik piratenpartei talk überwachung browser ajax clickjacking content-security-policy csp dell edellroot firefox html khtml konqueror maninthemiddle microsoft rss superfish vulnerability webcore xss ca certificateauthority sha2 symantec transvalid x509 blog calendar email english ipv6 kubik ludwigsburg lug lugbk openstreetmap planet rc2 schokokeks simplesharingextensions smime stadtmitte webinale 23c3 24c3 berlin bewußtsein c4 cctv copyright drm dvb freesoftware gpn6 gpn7 jugendumweltbewegung jukss kongress königswusterhausen licenses mysmartgrid ökologie papierlos philosophie privacy programmieren publicdomain querfunk radio rsaoaep rsapss science slides stuttgart surveillance theory tpm überwachungskameras wahl wahlcomputer wahlmaschinen wiki cccamp cccamp15 mitm cccamp11 openleaks taz chrome berserk bleichenbacher chromium crash diffiehellman forwardsecrecy keyexchange nss poodle cve ghost glibc redhat cmi deolalikar math milleniumproblems pnp provablesecurity augsburg beryl compizfusion composite inkscape kde lit07 luga waiblingen core coredump segfault webroot webserver crypto http 129a adresse agb antigenozidbewegung aok ard bahn bundestag bundesverfassungsgericht bürgerrechte bverfg datamining dataretention db demonstration diy einkaufen fernsehen frankfurt freedomnotfear freiheitstattangst fricard gez hausdurchsuchung humanistischeunion ice innenpolitik jugendschutz justiz kamera kameraüberwachung key köln metis mobil ninahagen optoutday ör osm peterschaar privatsphäre re-publica re-publica09 rechtsbeugung reklame religion rfid richtervorbehalt rp09 schäuble schlüssel spam steuerid steuernummer thermen topberlin uni verfassungsgericht verschlüsselung verschwörungstheorien verwertungsgesellschaft vgwort videoüberwachung vorratsdatenspeicherung werbung wga zdf zigaretten zigarettenautomaten distributions fma86t hardware wlan diploma diplomarbeit gsoc thesis university abuse boranet botnet ddos etymologie lg ncable sprache virus aead aes cfb cms gajim jabber joomla otr owncloud update xmpp babelfish camera canon china chinese csrf gadgets gammu gnokii googletranslate gphoto josm journalist language mandarin media merkaartor mobile moodle nokia ptp russia russian s9y time translation travel universaltranslator writing enigma film homosexualität turing addresssanitizer asan bufferoverflow c censorship clang developer france freedomofspeech gcc gebabbel gps gpsbabel idn iputils lenovo libressl memorysafety mobiletrailexplorer nancy openbsd ping politics rmll thinkpad useafterfree x1carbon zensur factoring keyserver revoke nist sha512 wordpress administration howto iptables network proxy rfc squid adguard antivirus breach cookies crime freak heist kaspersky komodia netfiltersdk privdog protocolfilters samesite bigbluebutton cookie fileexfiltration jodconverter libreoffice openid openidconnect sso azure bypass domain escapa ftp gobi google helma lemmings modulobias mozilla mpaa newspaper password passwordalert random salinecourier subdomain xsa adobe auskunftsanspruch botnetz bsi bugtracker bundesdatenschutzgesetz github nextcloud passwort sicherheit staatsanwaltschaft zugangsdaten 1und1 artikel ati augsburgerallgemeine backnang bash bios bonn cardreader chemnitz cinelerra clt compression console cpu cpufreq creativecommons delilinux demoscene desktop developingworld distribution dmidecode driver eltorito esslingen exe ffmpeg frankreich freeculture freedesktop freifunk frequencies froscon froscon2007 gaia gatos gnome googleearth graphics grub gtk harddisk hddtemp heartbleed homebrew hp ibm ico icons icoutils installparty iso itu kgtk kubuntu lessig license lm_sensors lpi lpic lspci lsusb macos mandriva memdisk memorystick messe metisse motherboard movie mplayer multimedia nouveau nvidia olpc omnibook opengl overheatd overheating pciids pcmagazin pcmcia presse qt r300 radeon randr12 rar reverseengineering ricoh samsung sd sdricohcs shellshock siegburg smart smartmontools sncf softwarefreedomday standards support syslinux t61 thesource theunarchiver tv tvout unar usability usb usbids vc-1 video videoediting vista wii wiibrew win32codecs windows windowsrefund wmv wos wos4 wrestool zeitung wiesbadenerkurier afl americanfuzzylop fuzzing 27c3 cellular frequency fsfe gsm mobilephones openbsc openbts osmocombb wiretapping diplomathesis simple upgoerfive words 0days afra altushost antivir axfr barcamp bias bodensee bugbounty bundestrojaner busby cbc chcounter clamav code conflictofinterest dingens dns drupal eplus firewall freewvs gallery gimp git gnutls gstreamer hackerone hacking infoleak informationdisclosure internetscan ircbot luckythirteen malware mantis mephisto mysql napster nessus ntp ntpd onlinedurchsuchung openvas padding panda pdo phishing python rand rhein session shellbot snallygaster sniffing sqlinjection squirrelmail stacktrace study sunras tlsdate toendacms unicef vlc vulnerabilities webapps xine zerodays zzuf cedric provider yacy klima klimacamp strom stromsparen wachstum wirtschaftswachstum absturz atari blinkenlights brownbox cccs demokratie environment fsf k21 lightwerk mappus painstation patents plebiszit police policeviolence politik pong pongmechanik pongmythos protest publictransport rech retrogames s21 schuster softwarepatents stallman stuttgart21 traffic umwelt verkehr volksabstimmung wien wkv acid3 base64 css midori script webdesign webkit webstandards
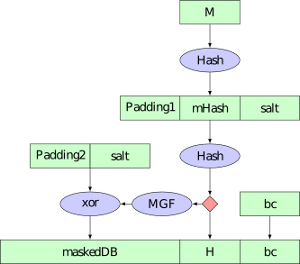 Die Verteidigung meiner
Die Verteidigung meiner 

