Entries tagged as rsa
Related tags
algorithm certificate cryptography eff observatory pss security ssl ca cacert ccc certificateauthority encryption hash https md5 openssl privatekey sha1 sha2 sha256 symantec tls transvalid x509 aiglx blog calendar come2linux compiz email english essen games ipv6 karlsruhe kubik linux ludwigsburg lug lugbk openstreetmap planet rc2 schokokeks serendipity simplesharingextensions smime stadtmitte web20 webinale webmontag wine xgl 23c3 24c3 4k assembler berlin bewußtsein braunschweig bsideshn c4 cctv copyright darmstadt datenschutz drm dvb easterhegg entropia freesoftware gpn gpn5 gpn6 gpn7 hacker hannover jugendumweltbewegung jukss kongress königswusterhausen licenses mrmcd mrmcd100b mrmcd101b mysmartgrid ökologie papierlos passwörter pgp philosophie privacy programmieren programming publicdomain querfunk radio rsaoaep rsapss science server slides stuttgart surveillance talk theory tpm überwachung überwachungskameras unicode utf-8 vortrag wahl wahlcomputer wahlmaschinen wiesbaden wiki android browser cccamp11 cloudflare dell edellroot facebook maninthemiddle openleaks superfish taz updates vulnerability windowsxp 68 aacs abmahnung alecempire aliens amusementpark art asia asia2013 banksy barrierefrei beijing berneconvention bittorrent bitv blueray boluo brigittezypries buch bücher bundestag cedric chaosradio china cinderella copycat corruptibles cpdl creativecommons culturalflatrate culture demonstration di disney disneyland ebook epetition eu eucopyrightdirective evrimsen fake fanart fanfiction filesharing film freeculture freifunk freizeitpark frequencies funkerspuk gema gemavermutung geodaten graffiti guangzhou gutenberg gvl hallstatt hddvd hiddenfrontier html huizhou ifpi illegalart iromance itu jankroemer journalismus justizministerium kinderlieder kopierschutz kriegderwelten kts kultur laterne laternenumzug lessig luoyang markenrecht metis movies mpaa musik musikindustrie musikpiraten negativland netradio nocopy patent patente penguinbooks petition piratbyrån piratebay politik presse pressefreiheit radiopolitik raubdruck raubkopie remix sanktmartin savenetradio sciencefiction shijingshan spiritlevel startrek stepmania tagesschau thepiratebay tomcruise travel trip2011 trips tuxmas tuxmas07 usa usbstick verwertungsgesellschaft vgmusikeditionen vgwort vlc w3c warez webradio wipo wizo wos wos4 apache apt badkeys cccamp cccamp15 certificates chrome chromium cmi crash crypto deb debian deolalikar diffiehellman diploma diplomarbeit enigma fedora fortigate fortinet forwardsecrecy gentoo gnupg gpg gsoc http itsecurity javascript key keyexchange keyserver leak letsencrypt libressl math milleniumproblems mitm modulobias nginx nist nss ocsp ocspstapling openbsd openid openidconnect openpgp packagemanagement password pnp provablesecurity random revocation revoke rpm schlüssel sha512 signatures sso thesis ubuntu university verschlüsselung web websecurity wordpress factoring aok berserk bleichenbacher firefox poodle addresssanitizer afl americanfuzzylop bash bufferoverflow fuzzing heartbleed shellshock sni gajim jabber otr xmpp michaelshart projectgutenberg diplomathesis language simple upgoerfive words 0days 27c3 adguard adobe aead aes afra altushost antivir antivirus asan auskunftsanspruch axfr azure barcamp bias bigbluebutton bodensee botnetz bsi bugbounty bundesdatenschutzgesetz bundestrojaner bundesverfassungsgericht busby bypass c cbc cellular cfb chcounter clamav clang clickjacking cms code conflictofinterest cookie csrf cve dingens distributions dns domain drupal eplus fileexfiltration firewall freak freewvs frequency fsfe ftp gallery gcc ghost gimp git glibc gnutls gobi google gsm gstreamer hackerone hacking helma infoleak informationdisclosure internetscan ircbot jodconverter joomla kaspersky komodia libreoffice luckythirteen malware mantis memorysafety mephisto microsoft mobilephones moodle mozilla mplayer multimedia mysql napster nessus netfiltersdk newspaper ntp ntpd onlinedurchsuchung openbsc openbts openvas osmocombb owncloud padding panda passwordalert passwort pdo phishing php privdog protocolfilters python rand redhat rhein rss s9y salinecourier session shellbot sicherheit snallygaster sniffing spam sqlinjection squirrelmail staatsanwaltschaft stacktrace study subdomain sunras support tlsdate toendacms unicef update useafterfree userdir virus vulnerabilities webapps windows wiretapping xine xsa xss zerodays zugangsdaten zzuf breach cookies crime heist samesite timeThursday, July 20. 2017
How I tricked Symantec with a Fake Private Key
 Lately, some attention was drawn to a widespread problem with TLS certificates. Many people are accidentally publishing their private keys. Sometimes they are released as part of applications, in Github repositories or with common filenames on web servers.
Lately, some attention was drawn to a widespread problem with TLS certificates. Many people are accidentally publishing their private keys. Sometimes they are released as part of applications, in Github repositories or with common filenames on web servers.If a private key is compromised, a certificate authority is obliged to revoke it. The Baseline Requirements – a set of rules that browsers and certificate authorities agreed upon – regulate this and say that in such a case a certificate authority shall revoke the key within 24 hours (Section 4.9.1.1 in the current Baseline Requirements 1.4.8). These rules exist despite the fact that revocation has various problems and doesn’t work very well, but that’s another topic.
I reported various key compromises to certificate authorities recently and while not all of them reacted in time, they eventually revoked all certificates belonging to the private keys. I wondered however how thorough they actually check the key compromises. Obviously one would expect that they cryptographically verify that an exposed private key really is the private key belonging to a certificate.
I registered two test domains at a provider that would allow me to hide my identity and not show up in the whois information. I then ordered test certificates from Symantec (via their brand RapidSSL) and Comodo. These are the biggest certificate authorities and they both offer short term test certificates for free. I then tried to trick them into revoking those certificates with a fake private key.
Forging a private key
To understand this we need to get a bit into the details of RSA keys. In essence a cryptographic key is just a set of numbers. For RSA a public key consists of a modulus (usually named N) and a public exponent (usually called e). You don’t have to understand their mathematical meaning, just keep in mind: They’re nothing more than numbers.
An RSA private key is also just numbers, but more of them. If you have heard any introductory RSA descriptions you may know that a private key consists of a private exponent (called d), but in practice it’s a bit more. Private keys usually contain the full public key (N, e), the private exponent (d) and several other values that are redundant, but they are useful to speed up certain things. But just keep in mind that a public key consists of two numbers and a private key is a public key plus some additional numbers. A certificate ultimately is just a public key with some additional information (like the host name that says for which web page it’s valid) signed by a certificate authority.
A naive check whether a private key belongs to a certificate could be done by extracting the public key parts of both the certificate and the private key for comparison. However it is quite obvious that this isn’t secure. An attacker could construct a private key that contains the public key of an existing certificate and the private key parts of some other, bogus key. Obviously such a fake key couldn’t be used and would only produce errors, but it would survive such a naive check.
I created such fake keys for both domains and uploaded them to Pastebin. If you want to create such fake keys on your own here’s a script. To make my report less suspicious I searched Pastebin for real, compromised private keys belonging to certificates. This again shows how problematic the leakage of private keys is: I easily found seven private keys for Comodo certificates and three for Symantec certificates, plus several more for other certificate authorities, which I also reported. These additional keys allowed me to make my report to Symantec and Comodo less suspicious: I could hide my fake key report within other legitimate reports about a key compromise.
Symantec revoked a certificate based on a forged private key
 Comodo didn’t fall for it. They answered me that there is something wrong with this key. Symantec however answered me that they revoked all certificates – including the one with the fake private key.
Comodo didn’t fall for it. They answered me that there is something wrong with this key. Symantec however answered me that they revoked all certificates – including the one with the fake private key.No harm was done here, because the certificate was only issued for my own test domain. But I could’ve also fake private keys of other peoples' certificates. Very likely Symantec would have revoked them as well, causing downtimes for those sites. I even could’ve easily created a fake key belonging to Symantec’s own certificate.
The communication by Symantec with the domain owner was far from ideal. I first got a mail that they were unable to process my order. Then I got another mail about a “cancellation request”. They didn’t explain what really happened and that the revocation happened due to a key uploaded on Pastebin.
I then informed Symantec about the invalid key (from my “real” identity), claiming that I just noted there’s something wrong with it. At that point they should’ve been aware that they revoked the certificate in error. Then I contacted the support with my “domain owner” identity and asked why the certificate was revoked. The answer: “I wanted to inform you that your FreeSSL certificate was cancelled as during a log check it was determined that the private key was compromised.”
To summarize: Symantec never told the domain owner that the certificate was revoked due to a key leaked on Pastebin. I assume in all the other cases they also didn’t inform their customers. Thus they may have experienced a certificate revocation, but don’t know why. So they can’t learn and can’t improve their processes to make sure this doesn’t happen again. Also, Symantec still insisted to the domain owner that the key was compromised even after I already had informed them that the key was faulty.
How to check if a private key belongs to a certificate?
 In case you wonder how you properly check whether a private key belongs to a certificate you may of course resort to a Google search. And this was fascinating – and scary – to me: I searched Google for “check if private key matches certificate”. I got plenty of instructions. Almost all of them were wrong. The first result is a page from SSLShopper. They recommend to compare the MD5 hash of the modulus. That they use MD5 is not the problem here, the problem is that this is a naive check only comparing parts of the public key. They even provide a form to check this. (That they ask you to put your private key into a form is a different issue on its own, but at least they have a warning about this and recommend to check locally.)
In case you wonder how you properly check whether a private key belongs to a certificate you may of course resort to a Google search. And this was fascinating – and scary – to me: I searched Google for “check if private key matches certificate”. I got plenty of instructions. Almost all of them were wrong. The first result is a page from SSLShopper. They recommend to compare the MD5 hash of the modulus. That they use MD5 is not the problem here, the problem is that this is a naive check only comparing parts of the public key. They even provide a form to check this. (That they ask you to put your private key into a form is a different issue on its own, but at least they have a warning about this and recommend to check locally.)Furthermore we get the same wrong instructions from the University of Wisconsin, Comodo (good that their engineers were smart enough not to rely on their own documentation), tbs internet (“SSL expert since 1996”), ShellHacks, IBM and RapidSSL (aka Symantec). A post on Stackexchange is the only result that actually mentions a proper check for RSA keys. Two more Stackexchange posts are not related to RSA, I haven’t checked their solutions in detail.
Going to Google results page two among some unrelated links we find more wrong instructions and tools from Symantec (Update 2020: Link offline), SSL247 (“Symantec Specialist Partner Website Security” - they learned from the best) and some private blog. A documentation by Aspera (belonging to IBM) at least mentions that you can check the private key, but in an unrelated section of the document. Also we get more tools that ask you to upload your private key and then not properly check it from SSLChecker.com, the SSL Store (Symantec “Website Security Platinum Partner”), GlobeSSL (“in SSL we trust”) and - well - RapidSSL.
Documented Security Vulnerability in OpenSSL
So if people google for instructions they’ll almost inevitably end up with non-working instructions or tools. But what about other options? Let’s say we want to automate this and have a tool that verifies whether a certificate matches a private key using OpenSSL. We may end up finding that OpenSSL has a function
x509_check_private_key() that can be used to “check the consistency of a private key with the public key in an X509 certificate or certificate request”. Sounds like exactly what we need, right?Well, until you read the full docs and find out that it has a BUGS section: “The check_private_key functions don't check if k itself is indeed a private key or not. It merely compares the public materials (e.g. exponent and modulus of an RSA key) and/or key parameters (e.g. EC params of an EC key) of a key pair.”
I think this is a security vulnerability in OpenSSL (discussion with OpenSSL here). And that doesn’t change just because it’s a documented security vulnerability. Notably there are downstream consumers of this function that failed to copy that part of the documentation, see for example the corresponding PHP function (the limitation is however mentioned in a comment by a user).
So how do you really check whether a private key matches a certificate?
Ultimately there are two reliable ways to check whether a private key belongs to a certificate. One way is to check whether the various values of the private key are consistent and then check whether the public key matches. For example a private key contains values p and q that are the prime factors of the public modulus N. If you multiply them and compare them to N you can be sure that you have a legitimate private key. It’s one of the core properties of RSA that it’s secure based on the assumption that it’s not feasible to calculate p and q from N.
You can use OpenSSL to check the consistency of a private key:
openssl rsa -in [privatekey] -checkFor my forged keys it will tell you:
RSA key error: n does not equal p qYou can then compare the public key, for example by calculating the so-called SPKI SHA256 hash:
openssl pkey -in [privatekey] -pubout -outform der | sha256sumopenssl x509 -in [certificate] -pubkey |openssl pkey -pubin -pubout -outform der | sha256sumAnother way is to sign a message with the private key and then verify it with the public key. You could do it like this:
openssl x509 -in [certificate] -noout -pubkey > pubkey.pemdd if=/dev/urandom of=rnd bs=32 count=1openssl rsautl -sign -pkcs -inkey [privatekey] -in rnd -out sigopenssl rsautl -verify -pkcs -pubin -inkey pubkey.pem -in sig -out checkcmp rnd checkrm rnd check sig pubkey.pemIf cmp produces no output then the signature matches.
As this is all quite complex due to OpenSSLs arcane command line interface I have put this all together in a script. You can pass a certificate and a private key, both in ASCII/PEM format, and it will do both checks.
Summary
Symantec did a major blunder by revoking a certificate based on completely forged evidence. There’s hardly any excuse for this and it indicates that they operate a certificate authority without a proper understanding of the cryptographic background.
Apart from that the problem of checking whether a private key and certificate match seems to be largely documented wrong. Plenty of erroneous guides and tools may cause others to fall for the same trap.
Update: Symantec answered with a blog post.
Posted by Hanno Böck
in Cryptography, English, Linux, Security
at
16:58
| Comments (12)
| Trackback (1)
Defined tags for this entry: ca, certificate, certificateauthority, openssl, privatekey, rsa, ssl, symantec, tls, x509
Sunday, May 17. 2015
About the supposed factoring of a 4096 bit RSA key
 tl;dr News about a broken 4096 bit RSA key are not true. It is just a faulty copy of a valid key.
tl;dr News about a broken 4096 bit RSA key are not true. It is just a faulty copy of a valid key.Earlier today a blog post claiming the factoring of a 4096 bit RSA key was published and quickly made it to the top of Hacker News. The key in question was the PGP key of a well-known Linux kernel developer. I already commented on Hacker News why this is most likely wrong, but I thought I'd write up some more details. To understand what is going on I have to explain some background both on RSA and on PGP keyservers. This by itself is pretty interesting.
RSA public keys consist of two values called N and e. The N value, called the modulus, is the interesting one here. It is the product of two very large prime numbers. The security of RSA relies on the fact that these two numbers are secret. If an attacker would be able to gain knowledge of these numbers he could use them to calculate the private key. That's the reason why RSA depends on the hardness of the factoring problem. If someone can factor N he can break RSA. For all we know today factoring is hard enough to make RSA secure (at least as long as there are no large quantum computers).
Now imagine you have two RSA keys, but they have been generated with bad random numbers. They are different, but one of their primes is the same. That means we have N1=p*q1 and N2=p*q2. In this case RSA is no longer secure, because calculating the greatest common divisor (GCD) of two large numbers can be done very fast with the euclidean algorithm, therefore one can calculate the shared prime value.
It is not only possible to break RSA keys if you have two keys with one shared factors, it is also possible to take a large set of keys and find shared factors between them. In 2012 Arjen Lenstra and his team published a paper using this attack on large scale key sets and at the same time Nadia Heninger and a team at the University of Michigan independently also performed this attack. This uncovered a lot of vulnerable keys on embedded devices, but these were mostly SSH and TLS keys. Lenstra's team however also found two vulnerable PGP keys. For more background you can watch this 29C3 talk by Nadia Heninger, Dan Bernstein and Tanja Lange.
PGP keyservers have been around since quite some time and they have a property that makes them especially interesting for this kind of research: They usually never delete anything. You can add a key to a keyserver, but you cannot remove it, you can only mark it as invalid by revoking it. Therefore using the data from the keyservers gives you a large set of cryptographic keys.
Okay, so back to the news about the supposedly broken 4096 bit key: There is a service called Phuctor where you can upload a key and it'll check it against a set of known vulnerable moduli. This service identified the supposedly vulnerable key.
The key in question has the key id e99ef4b451221121 and belongs to the master key bda06085493bace4. Here is the vulnerable modulus:
c844a98e3372d67f 562bd881da8ea66c a71df16deab1541c e7d68f2243a37665 c3f07d3dd6e651cc d17a822db5794c54 ef31305699a6c77c 043ac87cafc022a3 0a2a717a4aa6b026 b0c1c818cfc16adb aae33c47b0803152 f7e424b784df2861 6d828561a41bdd66 bd220cb46cd288ce 65ccaf9682b20c62 5a84ef28c63e38e9 630daa872270fa15 80cb170bfc492b80 6c017661dab0e0c9 0a12f68a98a98271 82913ff626efddfb f8ae8f1d40da8d13 a90138686884bad1 9db776bb4812f7e3 b288b47114e486fa 2de43011e1d5d7ca 8daf474cb210ce96 2aafee552f192ca0 32ba2b51cfe18322 6eb21ced3b4b3c09 362b61f152d7c7e6 51e12651e915fc9f 67f39338d6d21f55 fb4e79f0b2be4d49 00d442d567bacf7b 6defcd5818b050a4 0db6eab9ad76a7f3 49196dcc5d15cc33 69e1181e03d3b24d a9cf120aa7403f40 0e7e4eca532eac24 49ea7fecc41979d0 35a8e4accea38e1b 9a33d733bea2f430 362bd36f68440ccc 4dc3a7f07b7a7c8f cdd02231f69ce357 4568f303d6eb2916 874d09f2d69e15e6 33c80b8ff4e9baa5 6ed3ace0f65afb43 60c372a6fd0d5629 fdb6e3d832ad3d33 d610b243ea22fe66 f21941071a83b252 201705ebc8e8f2a5 cc01112ac8e43428 50a637bb03e511b2 06599b9d4e8e1ebc eb1e820d569e31c5 0d9fccb16c41315f 652615a02603c69f e9ba03e78c64fecc 034aa783adea213b
In fact this modulus is easily factorable, because it can be divided by 3. However if you look at the master key bda06085493bace4 you'll find another subkey with this modulus:
c844a98e3372d67f 562bd881da8ea66c a71df16deab1541c e7d68f2243a37665 c3f07d3dd6e651cc d17a822db5794c54 ef31305699a6c77c 043ac87cafc022a3 0a2a717a4aa6b026 b0c1c818cfc16adb aae33c47b0803152 f7e424b784df2861 6d828561a41bdd66 bd220cb46cd288ce 65ccaf9682b20c62 5a84ef28c63e38e9 630daa872270fa15 80cb170bfc492b80 6c017661dab0e0c9 0a12f68a98a98271 82c37b8cca2eb4ac 1e889d1027bc1ed6 664f3877cd7052c6 db5567a3365cf7e2 c688b47114e486fa 2de43011e1d5d7ca 8daf474cb210ce96 2aafee552f192ca0 32ba2b51cfe18322 6eb21ced3b4b3c09 362b61f152d7c7e6 51e12651e915fc9f 67f39338d6d21f55 fb4e79f0b2be4d49 00d442d567bacf7b 6defcd5818b050a4 0db6eab9ad76a7f3 49196dcc5d15cc33 69e1181e03d3b24d a9cf120aa7403f40 0e7e4eca532eac24 49ea7fecc41979d0 35a8e4accea38e1b 9a33d733bea2f430 362bd36f68440ccc 4dc3a7f07b7a7c8f cdd02231f69ce357 4568f303d6eb2916 874d09f2d69e15e6 33c80b8ff4e9baa5 6ed3ace0f65afb43 60c372a6fd0d5629 fdb6e3d832ad3d33 d610b243ea22fe66 f21941071a83b252 201705ebc8e8f2a5 cc01112ac8e43428 50a637bb03e511b2 06599b9d4e8e1ebc eb1e820d569e31c5 0d9fccb16c41315f 652615a02603c69f e9ba03e78c64fecc 034aa783adea213b
You may notice that these look pretty similar. But they are not the same. The second one is the real subkey, the first one is just a copy of it with errors.
If you run a batch GCD analysis on the full PGP key server data you will find a number of such keys (Nadia Heninger has published code to do a batch GCD attack). I don't know how they appear on the key servers, I assume they are produced by network errors, harddisk failures or software bugs. It may also be that someone just created them in some experiment.
The important thing is: Everyone can generate a subkey to any PGP key and upload it to a key server. That's just the way the key servers work. They don't check keys in any way. However these keys should pose no threat to anyone. The only case where this could matter would be a broken implementation of the OpenPGP key protocol that does not check if subkeys really belong to a master key.
However you won't be able to easily import such a key into your local GnuPG installation. If you try to fetch this faulty sub key from a key server GnuPG will just refuse to import it. The reason is that every sub key has a signature that proves that it belongs to a certain master key. For those faulty keys this signature is obviously wrong.
Now here's my personal tie in to this story: Last year I started a project to analyze the data on the PGP key servers. And at some point I thought I had found a large number of vulnerable PGP keys – including the key in question here. In a rush I wrote a mail to all people affected. Only later I found out that something was not right and I wrote to all affected people again apologizing. Most of the keys I thought I had found were just faulty keys on the key servers.
The code I used to parse the PGP key server data is public, I also wrote a background paper and did a talk at the BsidesHN conference.
Posted by Hanno Böck
in Code, Cryptography, English, Linux
at
22:46
| Comments (13)
| Trackbacks (4)
Thursday, October 27. 2011
Verteidigung meiner Diplomarbeit
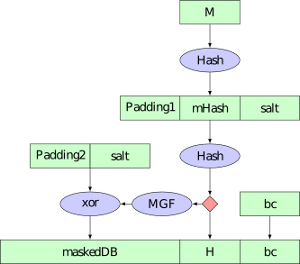 Die Verteidigung meiner Diplomarbeit über RSA-PSS an der HU Berlin wird am 10. November stattfinden. Die Veranstaltung ist öffentlich (17:00 Uhr s. t., Rudower Chausee 25, Campus Berlin-Adlershof, Raum 3'113). Achtung: Termin und Ort verschoben.
Die Verteidigung meiner Diplomarbeit über RSA-PSS an der HU Berlin wird am 10. November stattfinden. Die Veranstaltung ist öffentlich (17:00 Uhr s. t., Rudower Chausee 25, Campus Berlin-Adlershof, Raum 3'113). Achtung: Termin und Ort verschoben.Hier die Ankündigung:
Das Verschlüsselungs- und Signaturverfahren RSA ist das mit Abstand am häufigsten eingesetzte Public Key-Verfahren. RSA kann nicht in seiner ursprünglichen Form eingesetzt werden, da hierbei massive Sicherheitsprobleme auftreten. Zur Vorverarbeitung ist ein sogenanntes Padding notwendig. Bislang wird hierfür meist eine simple Hash-Funktion eingesetzt. Schon 1996 stellten Mihir Bellare und Philipp Rogaway für Signaturen ein verbessertes Verfahren mit dem Namen "Probabilistic Signature Scheme" (PSS) vor. Es garantiert unter bestimmten Annahmen "beweisbare" Sicherheit.
In der Diplomarbeit wurde untersucht, welche Vorteile RSA-PSS gegenüber früheren Verfahren bietet und inwieweit RSA-PSS in verbreiteten Protokollen bereits zum Einsatz kommt. Weiterhin wurde eine Implementierung des Verfahrens für X.509-Zertifikate für die nss-Bibliothek erstellt. nss wird unter anderem von Mozilla Firefox und Google Chrome eingesetzt.
Saturday, July 30. 2011
Using EFF SSL Observatory to find weak keys in CAcert

(c) EFF, Creative Commons by
I did some checks on the all_certs table selecting the certificates from cacert. I found out that there were 143 valid certificates with 512 bit. That is completely insecure and breakable by a home computer today. I also found that the majority of certificates still has 1024 bit, which by today's standards should be considered harmful - there have been no public breaks yet, but it's expected that it's possible to build an RSA-1024 cracker for an attacker with enough money.
I did the following query on the database:
SELECT RSA_Modulus_Bits, count(*) FROM all_certs WHERE `Validity:Not After datetime` > '2010-03-08' AND ( `Issuer` like '%CAcert.org%' OR `Issuer` like '%cacert.org') GROUP BY `RSA_Modulus_Bits` ORDER BY count(*);
+------------------+----------+
| RSA_Modulus_Bits | count(*) |
+------------------+----------+
[...]
| 512 | 143 |
| 4096 | 632 |
| 2048 | 3716 |
| 1024 | 5790 |
+------------------+----------+
Now, what further checks can we do? I checked for the RSA exponent. I found two certificates in the database with exponent 3. RSA with low exponent is also considered insecure, although one has to state that this is not a serious issue. RSA with low exponents is not insecure by itself, but it can create vulnerabilities in combination with other issues (if you're interested in details, read my diploma thesis).
I have not checked the CAcert database for the Debian SSL vulnerability, as that would've been non-trivial. There were scripts shipped with the SSL Observatory data, but I found them not easy to use, so I skipped that part.
My suggestions to cacert were to revoke all certificates with serious issues (like the 512 bit certificates). Also, I suggested that new certificates with insecure settings like RSA below 2048 bits or a low exponent should not be allowed. CAcert did most of this. By now, all 512 bit certificates should be revoked and it is impossible to create new ones below 1024 bit or with low exponents. It is however still possible to create 1024 bit certificates, which is due to a limitation in the client certificate creation script for the Internet Explorer. They say they're working on this and plan to prevent 1024 bit certificates in the future. They also told me that they've checked for the Debian SSL bug.
I've reported the issue on the 11th March and got a reply on the same day - that's pretty okay, one slight thing still: There was no security contact with a PGP key listed on the webpage (but I got a PGP-encrypted contact once I asked for it). That's not good, I expect especially from a security project that I can contact them for security issues with encrypted mail. One can also argue if four months is a bit long to fix such an issue, but as it was far away from being trivial, this can be apologized.
I'd say that I'm quite satisfied with the reactions of CAcert. I always got fast replies to questions I had and the issues were resolved in a proper way. I have other points of criticism on the security of CAcert, the issue that bothers me most is that they still use SHA-1 and refuse to switch to a more secure hashing algorithm like SHA-512, although all major browsers have support for this since a long time.
I want to encourage others to do further tests on CAcert. I'd like to see CAcert being an authority that does better than the commercial ones. The database from the observatory is a treasure and should be used by projects like CAcert to improve their security.
Wednesday, May 4. 2011
Diploma thesis on RSA-PSS finished
 Today I submitted my diploma thesis to my university.
Today I submitted my diploma thesis to my university.The thesis summarizes several months of investigation of the Probabilistic Signature Scheme (PSS). Traditionally, RSA signatures are done by hashing and then signing them. PSS is an improved, provable secure scheme to prepare a message before signing. The main focus was to investigate where PSS is implemented and used in real world cryptographic applications with a special focus on X.509.
During my work on that, I also implemented PSS signatures for the nss library in the Google Summer of Code 2010.
The thesis itself (including PDF and latex sources), patches for nss and everything else relevant can be found at
http://rsapss.hboeck.de.
Thursday, April 21. 2011
X.509 / SSL certificate test cases
https is likely the most widely used cryptographic protocol. It's based on X.509 certificates. There's a living debate how useful this concept is at all, mainly through the interesting findings of the EFF SSL Observatory. But that won't be my point today.
Pretty much all webpage certificates use RSA and sadly, the vast majority still use insecure hash algorithms. But it is rarely known that the X.509 standards support a whole bunch of other public key algorithms.
I've set up a page with a couple of test-cases for less-often used algorithm combinations. At the moment, it's mainly focused on RSASSA-PSS, but I plan to add elliptic curve algorithms soon. As I won't get any certificate authority to sign me certificates with anything else than classic RSA, I created my own testing root CA.
I'd be very interested to get some feedback. If you happen to have some interesting OS/Browser combination, please import the root certificate and send me a screenshot where I can see how many green ticks there are (post a link to the screenshot in the commends or send it via email).
At the moment, I'm especially looking for people to test:
Pretty much all webpage certificates use RSA and sadly, the vast majority still use insecure hash algorithms. But it is rarely known that the X.509 standards support a whole bunch of other public key algorithms.
I've set up a page with a couple of test-cases for less-often used algorithm combinations. At the moment, it's mainly focused on RSASSA-PSS, but I plan to add elliptic curve algorithms soon. As I won't get any certificate authority to sign me certificates with anything else than classic RSA, I created my own testing root CA.
I'd be very interested to get some feedback. If you happen to have some interesting OS/Browser combination, please import the root certificate and send me a screenshot where I can see how many green ticks there are (post a link to the screenshot in the commends or send it via email).
At the moment, I'm especially looking for people to test:
- Internet Explorer 9 on Windows 7
- Safari on latest MacOS X
- Internal browser on iPhone (I don't know if it's possible to install a new certificate authority there)
Saturday, February 26. 2011
Playing with the EFF SSL Observatory
The Electronic Frontier Foundation is running a fascinating project called the SSL Observatory. What they basically do is quite simple: They collected all SSL certificates they could get via https (by scanning all possible IPs), put them in a database and made statistics with them.
For an introduction, watch their talk at the 27C3 - it's worth it. For example, they found a couple of "Extended Validation"-Certificates that clearly violated the rules for extended validation, including one 512-bit EV-certificate.
The great thing is: They provide the full mysql database for download. I took the time to import the thing locally and am now able to run my own queries against it.
Let's show some examples: I'm interested in crypto algorithms used in the wild, so I wanted to know which are used in the wild at all. My query:
And the result:
This query was only for the valid certs, meaning they were signed by any browser-supported certificate authority. Now I run the same query on the all_certs table, which contains every cert, including expired, self-signed or otherwise invalid ones:
For an introduction, watch their talk at the 27C3 - it's worth it. For example, they found a couple of "Extended Validation"-Certificates that clearly violated the rules for extended validation, including one 512-bit EV-certificate.
The great thing is: They provide the full mysql database for download. I took the time to import the thing locally and am now able to run my own queries against it.
Let's show some examples: I'm interested in crypto algorithms used in the wild, so I wanted to know which are used in the wild at all. My query:
SELECT `Signature Algorithm`, count(*) FROM valid_certs GROUP BY `Signature Algorithm` ORDER BY count(*);shows all signature algorithms used on the certificates.
And the result:
+--------------------------+----------+Nothing very surprising here. Seems nobody is using anything else than RSA. The most popular hash algorithm is SHA-1, followed by MD5. The transition to SHA-256 seems to go very slowly (btw., the most common argument I heared when asking CAs for SHA-256 certificates was that Windows XP before service pack 3 doesn't support that). The four MD2-certificates seem interesting, though even that old, it's still more secure than MD5 and provides a similar security margin as SHA-1, though support for it has been removed from a couple of security libraries some time ago.
| Signature Algorithm | count(*) |
+--------------------------+----------+
| sha512WithRSAEncryption | 1 |
| sha1WithRSA | 1 |
| md2WithRSAEncryption | 4 |
| sha256WithRSAEncryption | 62 |
| md5WithRSAEncryption | 29958 |
| sha1WithRSAEncryption | 1503333 |
+--------------------------+----------+
This query was only for the valid certs, meaning they were signed by any browser-supported certificate authority. Now I run the same query on the all_certs table, which contains every cert, including expired, self-signed or otherwise invalid ones:
+-------------------------------------------------------+----------+It seems quite some people are experimenting with DSA signatures. Interesting are the number of GOST-certificates. GOST was a set of cryptography standards by the former soviet union. Seems the number of people trying to use elliptic curves is really low (compared to the popularity they have and that if anyone cares for SSL performance, they may be a good catch). For the algorithms only showing numbers, 1.2.840.113549.1.1.10 is RSASSA-PSS (not detected by current openssl release versions), 1.3.6.1.4.1.5849.1.3.2 is also a GOST-variant (GOST3411withECGOST3410) and 1.2.840.113549.27.1.5 is unknown to google, so it must be something very special.
| Signature Algorithm | count(*) |
+-------------------------------------------------------+----------+
| 1.2.840.113549.27.1.5 | 1 |
| sha1 | 1 |
| dsaEncryption | 1 |
| 1.3.6.1.4.1.5849.1.3.2 | 1 |
| md5WithRSAEncryption ANDALSO md5WithRSAEncryption | 1 |
| ecdsa-with-Specified | 1 |
| dsaWithSHA1-old | 2 |
| itu-t ANDALSO itu-t | 2 |
| dsaWithSHA | 3 |
| 1.2.840.113549.1.1.10 | 4 |
| ecdsa-with-SHA384 | 5 |
| ecdsa-with-SHA512 | 5 |
| ripemd160WithRSA | 9 |
| md4WithRSAEncryption | 15 |
| sha384WithRSAEncryption | 24 |
| GOST R 34.11-94 with GOST R 34.10-94 | 25 |
| shaWithRSAEncryption | 50 |
| sha1WithRSAEncryption ANDALSO sha1WithRSAEncryption | 72 |
| rsaEncryption | 86 |
| md2WithRSAEncryption | 120 |
| GOST R 34.11-94 with GOST R 34.10-2001 | 378 |
| sha512WithRSAEncryption | 513 |
| sha256WithRSAEncryption | 2542 |
| dsaWithSHA1 | 2703 |
| sha1WithRSA | 60969 |
| md5WithRSAEncryption | 1354658 |
| sha1WithRSAEncryption | 4196367 |
+-------------------------------------------------------+----------+
Posted by Hanno Böck
in Computer culture, Cryptography, English, Science, Security
at
22:40
| Comments (0)
| Trackbacks (0)
Defined tags for this entry: algorithm, certificate, cryptography, eff, observatory, pss, rsa, security, ssl
Friday, May 14. 2010
Secure RSA padding: RSA-PSS
I got selected for this years Google Summer of Code with a project for the implementation of RSA-PSS in the nss library. RSA-PSS will also be the topic of my diploma thesis, so I thought I'd write some lines about it.
RSA is, as you may probably know, the most widely used public key cryptography algorithm. It can be used for signing and encryption, RSA-PSS is about signing (something similar, RSA-OAEP, exists for encryption, but that's not my main topic).
The formula for the RSA-algorithm is S = M^k mod N (S is the signature, M the input, k the private key and N the product of two big prime numbers). One important thing is that M is not the Message itself, but some encoding of the message. A simple way of doing this encoding is using a hash-function, for example SHA256. This is basically how old standards (like PKCS #1 1.5) worked. While no attacks exist against this scheme, it's believed that this can be improved. One reason is that while the RSA-function accepts an input of size N (which is the same length as the keysize, for example 2048/4096 bit), hash-functions usually produce much smaller inputs (something like 160/256 bit).
An improved scheme for that is the Probabilistic Signature Scheme (PSS), (Bellare/Rogaway 1996/1998). PSS is "provable secure". It does not mean that the outcoming algorithm is "provable secure" (that's impossible with today's math), but that the outcome is as secure as the input algorithm RSA and the used hash function (so-called "random oracle model"). A standard for PSS-encryption is PKCS #1 2.1 (republished as RFC 3447) So PSS in general is a good idea as a security measure, but as there is no real pressure to implement it, it's still not used very much. Just an example, the new DNSSEC ressource records just published last year still use the old PKCS #1 1.5 standard.
For SSL/TLS, standards to use PSS exist (RFC 4055, RFC 5756), but implementation is widely lacking. Just recently, openssl got support for PSS verification. The only implementation of signature creation I'm aware of is the java-library bouncycastle (yes, this forced me to write some lines of java code).
The nss library is used by the Mozilla products (Firefox, Thunderbird), so an implementation there is crucial for a more widespread use of PSS.
RSA is, as you may probably know, the most widely used public key cryptography algorithm. It can be used for signing and encryption, RSA-PSS is about signing (something similar, RSA-OAEP, exists for encryption, but that's not my main topic).
The formula for the RSA-algorithm is S = M^k mod N (S is the signature, M the input, k the private key and N the product of two big prime numbers). One important thing is that M is not the Message itself, but some encoding of the message. A simple way of doing this encoding is using a hash-function, for example SHA256. This is basically how old standards (like PKCS #1 1.5) worked. While no attacks exist against this scheme, it's believed that this can be improved. One reason is that while the RSA-function accepts an input of size N (which is the same length as the keysize, for example 2048/4096 bit), hash-functions usually produce much smaller inputs (something like 160/256 bit).
An improved scheme for that is the Probabilistic Signature Scheme (PSS), (Bellare/Rogaway 1996/1998). PSS is "provable secure". It does not mean that the outcoming algorithm is "provable secure" (that's impossible with today's math), but that the outcome is as secure as the input algorithm RSA and the used hash function (so-called "random oracle model"). A standard for PSS-encryption is PKCS #1 2.1 (republished as RFC 3447) So PSS in general is a good idea as a security measure, but as there is no real pressure to implement it, it's still not used very much. Just an example, the new DNSSEC ressource records just published last year still use the old PKCS #1 1.5 standard.
For SSL/TLS, standards to use PSS exist (RFC 4055, RFC 5756), but implementation is widely lacking. Just recently, openssl got support for PSS verification. The only implementation of signature creation I'm aware of is the java-library bouncycastle (yes, this forced me to write some lines of java code).
The nss library is used by the Mozilla products (Firefox, Thunderbird), so an implementation there is crucial for a more widespread use of PSS.
Posted by Hanno Böck
in Code, Cryptography, English, Linux, Security
at
23:22
| Comments (0)
| Trackbacks (0)
Monday, April 5. 2010
Easterhegg in Munich
 I visited this year's easterhegg in Munich. The easterhegg is an event by the chaos computer club.
I visited this year's easterhegg in Munich. The easterhegg is an event by the chaos computer club.I held a talk expressing some thoughts I had in mind for quite a long time about free licenses. The conclusion is mainly that I think it very often may make more sense to use public domain "licensing" instead of free licenses with restrictions. The slides can be downloaded here (video recording here in high quality / 1024x576 and here in lower quality / 640x360). Talk was in german, but the slides are english. I plan to write down a longer text about the subject, but I don't know when I'll find time for that.
I also had a 5 minute lightning-talk about RSA-PSS and RSA-OAEP, slides are here (german). I will probably write my diploma thesis about PSS, so you may read more about that here in the future.
From the other talks, I want to mention one because I think it's a very interesting project about an important topic: The mySmartGrid project is working on an opensource based solution for local smart grids. It's a research project by Fraunhofer ITWM Kaiserslautern and it sounds very promising. Smart grids will almost definitely come within the next years and if people stick to the solutions provided by big energy companies, this will most likely be a big thread to privacy and will most probably prefer old centralized electricity generation.
Posted by Hanno Böck
in Code, Computer culture, Copyright, Ecology, English, Politics, Security
at
20:58
| Comments (4)
| Trackbacks (0)
Defined tags for this entry: ccc, copyright, easterhegg, licenses, mysmartgrid, publicdomain, rsa, rsaoaep, rsapss
(Page 1 of 1, totaling 9 entries)